Peripateticism
Yuens' blog
优化CPU矩阵乘法
一步步优化GEMM。最终相比当初的naive矩阵乘法有近乎10倍的性能提升。用到的方法简单罗列如下:
- 寄存器变量:kernel中反复用的变量声明时带上register前缀;
- L2 cache:kernel中的数据复用;
- 指针代替索引:减少访问开销;
- 间接寻址代替直接寻址:减少每次for循环中指针的更新次数;
- simd:用上intel intrinsic实现一次完成1x4个C元素的乘加操作;
- 矩阵分块:设置分块参数,优化L2 cache的使用;
- 对kernel中参与计算的部分A和部分B打包:优化计算C元素时对A和B的访问。
到第7步后,就可以对已经写成intrinsic或者neon的代码,进一步写为汇编,又会有至少10~15%的性能提升。
下面就从头开始吧!
1. 最原始的矩阵乘法</h1>
首先,给出最原始的矩阵乘法的C实现:
/* Create macros so that the matrices are stored in column-major order */
#define A(i,j) a[ (j)*lda + (i) ]
#define B(i,j) b[ (j)*ldb + (i) ]
#define C(i,j) c[ (j)*ldc + (i) ]
/* Routine for computing C = A * B + C */
void REF_MMult( int m, int n, int k, double *a, int lda,
double *b, int ldb,
double *c, int ldc )
{
int i, j, p;
for ( i=0; i<m; i++ ){ /* Loop over the rows of C */
for ( j=0; j<n; j++ ){ /* Loop over the columns of C */
for ( p=0; p<k; p++ ){ /* Update C( i,j ) with the inner
product of the i-th row of A and
the j-th of B */
C( i,j ) = C( i,j ) + A( i,p ) * B( p,j );
}
}
}
}
其中,相乘的两个矩阵:矩阵A是m行k列,矩阵B是k行n列。
- 参考:矩阵乘法的四种理解方式 - lijiankou - 博客园 http://www.cnblogs.com/lijiankou/archive/2013/07/11/3183728.html
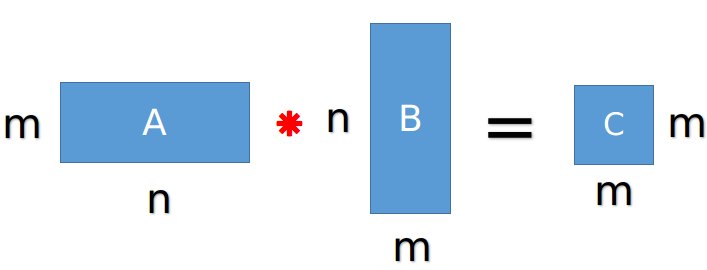 矩阵A和矩阵C相乘
矩阵A和矩阵C相乘
该方法是操作的是一维数组,通过行列索引i、j、p(分别遍历m、n、p)以及lda、ldb、ldc(本身这三个就是与m、n、k是等价,相当于矩阵A、B、C的每行元素的个数)来实现对二维矩阵下标的控制。
#define A(i,j) a[ (j)*lda + (i) ]
#define B(i,j) b[ (j)*ldb + (i) ]
#define C(i,j) c[ (j)*ldc + (i) ]
这里使用了带参数的宏定义,带参宏定义的一般形式为:#define 宏名(形参列表) 字符串。对带参数的宏,在调用中,不仅要宏展开,而且要用实参去代换形参。三点说明:
- 1. 带参宏定义中,形参之间可以出现空格,但是宏名和形参列表之间不能有空格出现;
- 2. 在带参宏定义中,不会为形式参数分配内存,因此不必指明数据类型。而在宏调用中,实参包含了具体的数据,要用它们去代换形参,因此必须指明数据类型; 这一点和函数是不同的:在函数中,形参和实参是两个不同的变量,都有自己的作用域,调用时要把实参的值传递给形参;而在带参数的宏中,只是符号的替换,不存在值传递的问题。
- 3. 在宏定义中,字符串内的形参通常要用括号括起来以避免出错。
- 参考:C语言带参数宏定义_C语言中文网 http://c.biancheng.net/cpp/html/66.html
所以宏定义中以及i、j、p的三个循环次数m、n、k可以看出,该方法是采用列优先存储。我是这么看的:矩阵A的宏定义是#define A(i,j) a[ (j)*lda + (i) ],查看对应for循环的代码,第一个for循环就是用i来遍历m,那么既然
1.1 行优先与列优先
行优先或者列优先没有好坏,但其直接涉及到对内存中数据的最佳存储访问方式。因为在内存使用上,程序访问的内存地址之间连续性越好,程序的访问效率就越高。所以应该尽量在行优先机制的编译器,比如C/C++,CUDA等等上,采用行优先的数据存储方式;在列优先机制的编译器,比如Fortune, Matlab等等上,采用列优先的数据存储方式。但这种思想渗透到编程中之后,代码的质量就会提高一个档次。
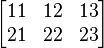 现在有2行三列矩阵
现在有2行三列矩阵
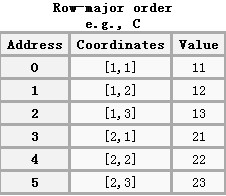
该矩阵对应的行优先序(从第一行开始存储,再存储第二行以此类推)
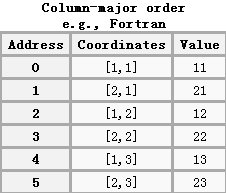
该矩阵对应的列优先序(从第一列开始存储,再存储第二列以此类推)
- 参考:C语言行优先和列优先的问题深入分析_C 语言_脚本之家 http://www.jb51.net/article/101882.htm
- 列优先与行优先 - For record - 博客频道 - CSDN.NET http://blog.csdn.net/shenck1992/article/details/50041777
2. 第一次优化
/* Create macros so that the matrices are stored in column-major order */
#define A(i,j) a[ (j)*lda + (i) ]
#define B(i,j) b[ (j)*ldb + (i) ]
#define C(i,j) c[ (j)*ldc + (i) ]
/* Routine for computing C = A * B + C */
void AddDot( int, double *, int, double *, double * );
void MY_MMult( int m, int n, int k, double *a, int lda,
double *b, int ldb,
double *c, int ldc )
{
int i, j;
for ( j=0; j<n; j+=1 ){ /* Loop over the columns of C */
for ( i=0; i<m; i+=1 ){ /* Loop over the rows of C */
/* Update the C( i,j ) with the inner product of the ith row of A
and the jth column of B */
AddDot( k, &A( i,0 ), lda, &B( 0,j ), &C( i,j ) );
}
}
}
/* Create macro to let X( i ) equal the ith element of x */
#define X(i) x[ (i)*incx ]
void AddDot( int k, double *x, int incx, double *y, double *gamma )
{
/* compute gamma := x' * y + gamma with vectors x and y of length n.
Here x starts at location x with increment (stride) incx and y starts at location y and has (implicit) stride of 1.
*/
int p;
for ( p=0; p<k; p++ ){
*gamma += X( p ) * y[ p ];
}
}
大致结构上基本不变,由三重for循环变为两重(用i、j分别遍历n、m)。减少的第三重循环原本做的是通过A的第i行和B的第j列来更新C(i,j),当然改变后的代码使用了一个AddDot函数(取出A的一行,B的一列,点乘后加和)来代替第三重循环,不过把第三重循环放到了AddDot函数里来做。这样看起来更规整一些,改变前后性能只有很小的提升。
另外就是针对遍历C的两重循环的顺序改变了,现在变为先遍历C的列再遍历行,与之前相反。
3. 第二次优化
/* Create macros so that the matrices are stored in column-major order */
#define A(i,j) a[ (j)*lda + (i) ]
#define B(i,j) b[ (j)*ldb + (i) ]
#define C(i,j) c[ (j)*ldc + (i) ]
/* Routine for computing C = A * B + C */
void AddDot( int, double *, int, double *, double * );
void MY_MMult( int m, int n, int k, double *a, int lda,
double *b, int ldb,
double *c, int ldc )
{
int i, j;
for ( j=0; j<n; j+=4 ){ /* Loop over the columns of C, unrolled by 4 */
for ( i=0; i<m; i+=1 ){ /* Loop over the rows of C */
/* Update the C( i,j ) with the inner product of the ith row of A
and the jth column of B */
AddDot( k, &A( i,0 ), lda, &B( 0,j ), &C( i,j ) );
/* Update the C( i,j+1 ) with the inner product of the ith row of A
and the (j+1)th column of B */
AddDot( k, &A( i,0 ), lda, &B( 0,j+1 ), &C( i,j+1 ) );
/* Update the C( i,j+2 ) with the inner product of the ith row of A
and the (j+2)th column of B */
AddDot( k, &A( i,0 ), lda, &B( 0,j+2 ), &C( i,j+2 ) );
/* Update the C( i,j+3 ) with the inner product of the ith row of A
and the (j+1)th column of B */
AddDot( k, &A( i,0 ), lda, &B( 0,j+3 ), &C( i,j+3 ) );
}
}
}
/* Create macro to let X( i ) equal the ith element of x */
#define X(i) x[ (i)*incx ]
void AddDot( int k, double *x, int incx, double *y, double *gamma )
{
/* compute gamma := x' * y + gamma with vectors x and y of length n.
Here x starts at location x with increment (stride) incx and y starts at location y and has (implicit) stride of 1.
*/
int p;
for ( p=0; p<k; p++ ){
*gamma += X( p ) * y[ p ];
}
}
最明显改变就是4次AddDot函数(取出矩阵A的一行,矩阵B的一列,做先点乘后加和),即每次计算得到矩阵C的四个元素的值。这样相比之前,应该有不到4倍的性能提升。
1. 1x1到1x4
1.1 naive 1x1
#define A(i, j) a[k*(i) + (j)]
#define B(i, j) a[n*(i) + (j)]
#define C(i, j) a[n*(i) + (j)]
for(int i = 0; i < m; ++i)
{
for(int j = 0; j < n; ++j)
{
for(int p = 0; p < k; ++p)
{
C(i, j) += A(i, p) * B(p, j);
}
}
}
1.2 1x1
#define A(i, j) a[k*(i) + (j)]
#define B(i, j) a[n*(i) + (j)]
#define C(i, j) a[n*(i) + (j)]
for(int i = 0; i < m; ++i)
{
for(int j = 0; j < n; ++j)
{
AddDot(&A(i, 0), &B(0, j), &C(i, j), k, n);
}
}
#define B_COL(p) b_col[p*n]
AddDot(float *a_row, float *b_col, float *c, int k, int n)
{
for(int p = 0; p < k; ++p)
{
*c += a_row[p] * B_COL(p);
}
}
1.3 1x4
#define A(i, j) a[k*(i) + (j)]
#define B(i, j) a[n*(i) + (j)]
#define C(i, j) a[n*(i) + (j)]
for(int i = 0; i < m; ++i)
{
for(int j = 0; j < n; j+=4)
{
AddDot(&A(i, 0), &B(0, j+0), &C(i, j+0), k, n);
AddDot(&A(i, 0), &B(0, j+1), &C(i, j+1), k, n);
AddDot(&A(i, 0), &B(0, j+2), &C(i, j+2), k, n);
AddDot(&A(i, 0), &B(0, j+3), &C(i, j+3), k, n);
}
}
#define B_COL(p) b_col[p*n]
AddDot(float *a_row, float *b_col, float *c, int k, int n)
{
for(int p = 0; p < k; ++p)
{
*c += a_row[p] * B_COL(p);
}
}
1.4 1x4
#define A(i, j) a[k*(i) + (j)]
#define B(i, j) a[n*(i) + (j)]
#define C(i, j) a[n*(i) + (j)]
for(int i = 0; i < m; ++i)
{
for(int j = 0; j < n; j+=4)
{
AddDot1x4(&A(i, 0), &B(0, j), &C(i, j), k, n);
}
}
AddDot1x4(float *a_row, float *b_col, float *c, int k, int n)
{
for(int p = 0; p < k; ++p)
C(0, 0) += a_row[p] * B(p, 0);
for(int p = 0; p < k; ++p)
C(0, 1) += a_row[p] * B(p, 1);
for(int p = 0; p < k; ++p)
C(0, 2) += a_row[p] * B(p, 2);
for(int p = 0; p < k; ++p)
C(0, 3) += a_row[p] * B(p, 3);
}
1.5 1x4的提升 L2 Cache
规模m = n = k > 500左右时会有2倍的提升,因为原本的4个for循环合并为一个,一次for循环同时算4个C(i, j):
- 索引
p每8个浮点操作(4个乘法+加法)只需要更新一次; - 元素
A( 0, p )只需从内存中取出1次(不像前面取出4次),之后都在L2 cache中,直到后面的数填满了L2 cache。
#define A(i, j) a[k*(i) + (j)]
#define B(i, j) a[n*(i) + (j)]
#define C(i, j) a[n*(i) + (j)]
for(int i = 0; i < m; ++i)
{
for(int j = 0; j < n; j+=4)
{
AddDot1x4(&A(i, 0), &B(0, j), &C(i, j), k, n);
}
}
AddDot1x4(float *a_row, float *b_col, float *c, int k, int n)
{
for(int p = 0; p < k; ++p)
{
C(0, 0) += A(0, p) * B(p, 0);
C(0, 1) += A(0, p) * B(p, 1);
C(0, 2) += A(0, p) * B(p, 2);
C(0, 3) += A(0, p) * B(p, 3);
}
}
1.6 1x4的提升 C和A放到Register
规模m = n = k < 500时会有2倍的提升,因为把C的一行四列的1x4的计算临时结果以及A(p, 0)放到了寄存器中,减少了cache与register之间的数据传输。
#define A(i, j) a[k*(i) + (j)]
#define B(i, j) a[n*(i) + (j)]
#define C(i, j) a[n*(i) + (j)]
for(int i = 0; i < m; ++i)
{
for(int j = 0; j < n; j+=4)
{
AddDot1x4(&A(i, 0), &B(0, j), &C(i, j), k, n);
}
}
AddDot1x4(float *a_row, float *b_col, float *c, int k, int n)
{
register float
c_00_reg, c_01_reg, c_02_reg, c_03_reg,
a_0p_reg;
c_00_reg = 0.0;
c_01_reg = 0.0;
c_02_reg = 0.0;
c_03_reg = 0.0;
for(int p = 0; p < k; ++p)
{
a_0p_reg = A(0, p);
c_00_reg += a_0p_reg * B(p, 0);
c_01_reg += a_0p_reg * B(p, 1);
c_02_reg += a_0p_reg * B(p, 2);
c_03_reg += a_0p_reg * B(p, 3);
}
C(0, 0) = c_00_reg;
C(0, 1) = c_01_reg;
C(0, 2) = c_02_reg;
C(0, 3) = c_03_reg;
}
1.7 1x4的提升 用指针访问B
规模m = n = k < 500时会有1.5~2倍的提升,用指针访问B,bp0_pntr, bp1_pntr, bp2_pntr, and bp3_pntr 访问 B( p, 0 ), B( p, 1 ), B( p, 2 ), B( p, 3 ),减少数据索引找B中元素的开销。
#define A(i, j) a[k*(i) + (j)]
#define B(i, j) a[n*(i) + (j)]
#define C(i, j) a[n*(i) + (j)]
for(int i = 0; i < m; ++i)
{
for(int j = 0; j < n; j+=4)
{
AddDot1x4(&A(i, 0), &B(0, j), &C(i, j), k, n);
}
}
AddDot1x4(float *a_row, float *b_col, float *c, int k, int n)
{
register float
c_00_reg, c_01_reg, c_02_reg, c_03_reg,
a_0p_reg;
c_00_reg = 0.0;
c_01_reg = 0.0;
c_02_reg = 0.0;
c_03_reg = 0.0;
float
*bp0_pntr, *bp1_pntr, *bp2_pntr, *bp3_pntr;
bp0_pntr = &B( 0, 0 );
bp1_pntr = &B( 0, 1 );
bp2_pntr = &B( 0, 2 );
bp3_pntr = &B( 0, 3 );
for(int p = 0; p < k; ++p)
{
a_0p_reg = A(0, p);
c_00_reg += a_0p_reg * *bp0_pntr++;
c_01_reg += a_0p_reg * *bp1_pntr++;
c_02_reg += a_0p_reg * *bp2_pntr++;
c_03_reg += a_0p_reg * *bp3_pntr++;
}
C(0, 0) = c_00_reg;
C(0, 1) = c_01_reg;
C(0, 2) = c_02_reg;
C(0, 3) = c_03_reg;
}
1.8 1x4的轻微下降 对k方向展开p+=4,这个累加的数也可以自定
unroll这个for循环,从原本的+=1改为+=4混淆了编译器(unroll多少并非固定,可以根据不同的平台调节),反而有性能下降。
#define A(i, j) a[k*(i) + (j)]
#define B(i, j) a[n*(i) + (j)]
#define C(i, j) a[n*(i) + (j)]
for(int i = 0; i < m; ++i)
{
for(int j = 0; j < n; j+=4)
{
AddDot1x4(&A(i, 0), &B(0, j), &C(i, j), k, n);
}
}
AddDot1x4(float *a_row, float *b_col, float *c, int k, int n)
{
register float
c_00_reg, c_01_reg, c_02_reg, c_03_reg,
a_0p_reg;
c_00_reg = 0.0;
c_01_reg = 0.0;
c_02_reg = 0.0;
c_03_reg = 0.0;
float
*bp0_pntr, *bp1_pntr, *bp2_pntr, *bp3_pntr;
bp0_pntr = &B( 0, 0 );
bp1_pntr = &B( 0, 1 );
bp2_pntr = &B( 0, 2 );
bp3_pntr = &B( 0, 3 );
for(int p = 0; p < k; p+=4)
{
a_0p_reg = A(0, p);
c_00_reg += a_0p_reg * *bp0_pntr++;
c_01_reg += a_0p_reg * *bp1_pntr++;
c_02_reg += a_0p_reg * *bp2_pntr++;
c_03_reg += a_0p_reg * *bp3_pntr++;
a_0p_reg = A(0, p+1);
c_00_reg += a_0p_reg * *bp0_pntr++;
c_01_reg += a_0p_reg * *bp1_pntr++;
c_02_reg += a_0p_reg * *bp2_pntr++;
c_03_reg += a_0p_reg * *bp3_pntr++;
a_0p_reg = A(0, p+2);
c_00_reg += a_0p_reg * *bp0_pntr++;
c_01_reg += a_0p_reg * *bp1_pntr++;
c_02_reg += a_0p_reg * *bp2_pntr++;
c_03_reg += a_0p_reg * *bp3_pntr++;
a_0p_reg = A(0, p+3);
c_00_reg += a_0p_reg * *bp0_pntr++;
c_01_reg += a_0p_reg * *bp1_pntr++;
c_02_reg += a_0p_reg * *bp2_pntr++;
c_03_reg += a_0p_reg * *bp3_pntr++;
}
C(0, 0) = c_00_reg;
C(0, 1) = c_01_reg;
C(0, 2) = c_02_reg;
C(0, 3) = c_03_reg;
}
1.9 1x4 间接寻址(indirect addressing)
间接寻址操作如下:
c_00_reg += a_0p_reg * *(bp0_pntr+1);
bp0_pntr指向元素B( p, 0 )。因此bp0_pntr+1指向元素B( p+1, 0 ),间接访问这种方法不需要更新指针的地址,而是直接通过+1访问下一个元素。这样,每算4次,b指针才会被更新,通过间接寻址减少了指针变量的更新次数。
注:没有性能提升,因为编译器已经做了这样的优化,我们只是显式地写了出来。
#define A(i, j) a[k*(i) + (j)]
#define B(i, j) a[n*(i) + (j)]
#define C(i, j) a[n*(i) + (j)]
for(int i = 0; i < m; ++i)
{
for(int j = 0; j < n; j+=4)
{
AddDot1x4(&A(i, 0), &B(0, j), &C(i, j), k, n);
}
}
AddDot1x4(float *a_row, float *b_col, float *c, int k, int n)
{
register float
c_00_reg, c_01_reg, c_02_reg, c_03_reg,
a_0p_reg;
c_00_reg = 0.0;
c_01_reg = 0.0;
c_02_reg = 0.0;
c_03_reg = 0.0;
float
*bp0_pntr, *bp1_pntr, *bp2_pntr, *bp3_pntr;
bp0_pntr = &B( 0, 0 );
bp1_pntr = &B( 0, 1 );
bp2_pntr = &B( 0, 2 );
bp3_pntr = &B( 0, 3 );
for(int p = 0; p < k; p+=4)
{
a_0p_reg = A(0, p);
c_00_reg += a_0p_reg * *bp0_pntr;
c_01_reg += a_0p_reg * *bp1_pntr;
c_02_reg += a_0p_reg * *bp2_pntr;
c_03_reg += a_0p_reg * *bp3_pntr;
a_0p_reg = A(0, p+1);
c_00_reg += a_0p_reg * *(bp0_pntr+1);
c_01_reg += a_0p_reg * *(bp1_pntr+1);
c_02_reg += a_0p_reg * *(bp2_pntr+1);
c_03_reg += a_0p_reg * *(bp3_pntr+1);
a_0p_reg = A(0, p+2);
c_00_reg += a_0p_reg * *(bp0_pntr+2);
c_01_reg += a_0p_reg * *(bp1_pntr+2);
c_02_reg += a_0p_reg * *(bp2_pntr+2);
c_03_reg += a_0p_reg * *(bp3_pntr+2);
a_0p_reg = A(0, p+3);
c_00_reg += a_0p_reg * *(bp0_pntr+3);
c_01_reg += a_0p_reg * *(bp1_pntr+3);
c_02_reg += a_0p_reg * *(bp2_pntr+3);
c_03_reg += a_0p_reg * *(bp3_pntr+3);
bp0_pntr+=4;
bp1_pntr+=4;
bp2_pntr+=4;
bp3_pntr+=4;
}
C(0, 0) = c_00_reg;
C(0, 1) = c_01_reg;
C(0, 2) = c_02_reg;
C(0, 3) = c_03_reg;
}
2. 1x4到4x4
后面使用到向量指令以及向量寄存器,做到一次算4x4个结果。
- 有一部分特殊指令集如SSE3,一个周期内可执行两个乘加操作(两个乘法和两个加法操作),也就是每个周期可对4个浮点操作;
- 要把数据放到向量寄存器(vector register)才能实现如此操作;
因为有16个向量寄存器,每个都可以存放两个双精度double或四个单精度的浮点数。因而可以将32个双精度浮数点或64个单精度浮点数放到这16个向量寄存器中,若是双精度即我们4x4大小的矩阵C的元素,若是单精度即可以放8x8规模大小的矩阵C的元素。
2.1 4x4 A的行 B的列 每次取4
扩展AddDot,每次取A的4行,B的4列,在AddDot4x4中计算16个C元素。
#define A(i, j) a[k*(i) + (j)]
#define B(i, j) a[n*(i) + (j)]
#define C(i, j) a[n*(i) + (j)]
for(int i = 0; i < m; i+=4)
{
for(int j = 0; j < n; j+=4)
{
AddDot4x4(&A(i, 0), &B(0, j), &C(i, j), n, k);
}
}
void AddDot4x4(float *a, float *b, float *c, const int n, const int k)
{
/* So, this routine computes a 4x4 block of matrix A
C( 0, 0 ), C( 0, 1 ), C( 0, 2 ), C( 0, 3 ).
C( 1, 0 ), C( 1, 1 ), C( 1, 2 ), C( 1, 3 ).
C( 2, 0 ), C( 2, 1 ), C( 2, 2 ), C( 2, 3 ).
C( 3, 0 ), C( 3, 1 ), C( 3, 2 ), C( 3, 3 ).
Notice that this routine is called with c = C( i, j ) in the
previous routine, so these are actually the elements
C( i , j ), C( i , j+1 ), C( i , j+2 ), C( i , j+3 )
C( i+1, j ), C( i+1, j+1 ), C( i+1, j+2 ), C( i+1, j+3 )
C( i+2, j ), C( i+2, j+1 ), C( i+2, j+2 ), C( i+2, j+3 )
C( i+3, j ), C( i+3, j+1 ), C( i+3, j+2 ), C( i+3, j+3 )
in the original matrix C
In this version, we "inline" AddDot */
// 1st row of C
AddDot(&A(0, 0), &B(0, 0), &C(0, 0), k, n);
AddDot(&A(0, 0), &B(0, 1), &C(0, 1), k, n);
AddDot(&A(0, 0), &B(0, 2), &C(0, 2), k, n);
AddDot(&A(0, 0), &B(0, 3), &C(0, 3), k, n);
// 2rd row of C
AddDot(&A(1, 0), &B(0, 0), &C(1, 0), k, n);
AddDot(&A(1, 0), &B(0, 1), &C(1, 1), k, n);
AddDot(&A(1, 0), &B(0, 2), &C(1, 2), k, n);
AddDot(&A(1, 0), &B(0, 3), &C(1, 3), k, n);
// 3nd row of C
AddDot(&A(2, 0), &B(0, 0), &C(2, 0), k, n);
AddDot(&A(2, 0), &B(0, 1), &C(2, 1), k, n);
AddDot(&A(2, 0), &B(0, 2), &C(2, 2), k, n);
AddDot(&A(2, 0), &B(0, 3), &C(2, 3), k, n);
// 4th row of C
AddDot(&A(3, 0), &B(0, 0), &C(3, 0), k, n);
AddDot(&A(3, 0), &B(0, 1), &C(3, 1), k, n);
AddDot(&A(3, 0), &B(0, 2), &C(3, 2), k, n);
AddDot(&A(3, 0), &B(0, 3), &C(3, 3), k, n);
}
#define B_COL(p) b_col[p*n]
void AddDot(float *a_row, float *b_col, float *c, int k, int n)
{
for(int p = 0; p < k; ++p)
{
*c += a_row[p] * B_COL(p);
}
}
2.2 4x4 拆分AddDot到AddDot4x4中
无性能提升。
#define A(i, j) a[k*(i) + (j)]
#define B(i, j) a[n*(i) + (j)]
#define C(i, j) a[n*(i) + (j)]
for(int i = 0; i < m; i+=4)
{
for(int j = 0; j < n; j+=4)
{
AddDot4x4(&A(i, 0), &B(0, j), &C(i, j), n, k);
}
}
void AddDot4x4(float *a, float *b, float *c, const int n, const int k)
{
// 1st row of C
for(int p = 0; p < k; ++p)
C(0, 0) += A(0, p) * B(p, 0);
for(int p = 0; p < k; ++p)
C(0, 1) += A(0, p) * B(p, 1);
for(int p = 0; p < k; ++p)
C(0, 2) += A(0, p) * B(p, 2);
for(int p = 0; p < k; ++p)
C(0, 3) += A(0, p) * B(p, 3);
// 2rd row of C
for(int p = 0; p < k; ++p)
C(1, 0) += A(1, p) * B(p, 0);
for(int p = 0; p < k; ++p)
C(1, 1) += A(1, p) * B(p, 1);
for(int p = 0; p < k; ++p)
C(1, 2) += A(1, p) * B(p, 2);
for(int p = 0; p < k; ++p)
C(1, 3) += A(1, p) * B(p, 3);
// 3nd row of C
for(int p = 0; p < k; ++p)
C(2, 0) += A(2, p) * B(p, 0);
for(int p = 0; p < k; ++p)
C(2, 1) += A(2, p) * B(p, 1);
for(int p = 0; p < k; ++p)
C(2, 2) += A(2, p) * B(p, 2);
for(int p = 0; p < k; ++p)
C(2, 3) += A(2, p) * B(p, 3);
// 4th row of C
for(int p = 0; p < k; ++p)
C(3, 0) += A(3, p) * B(p, 0);
for(int p = 0; p < k; ++p)
C(3, 1) += A(3, p) * B(p, 1);
for(int p = 0; p < k; ++p)
C(3, 2) += A(3, p) * B(p, 2);
for(int p = 0; p < k; ++p)
C(3, 3) += A(3, p) * B(p, 3);
}
2.3 4x4 提升 合并AddDot4x4中的For循环
在m=n=k>500时,4~5倍的性能提升,合并16个For循环为1个。
矩阵变更大,不少数据在寄存器中可被复用地更多。
#define A(i, j) a[k*(i) + (j)]
#define B(i, j) a[n*(i) + (j)]
#define C(i, j) a[n*(i) + (j)]
for(int i = 0; i < m; i+=4)
{
for(int j = 0; j < n; j+=4)
{
AddDot4x4(&A(i, 0), &B(0, j), &C(i, j), n, k);
}
}
void AddDot4x4(float *a, float *b, float *c, const int n, const int k)
{
for(int p = 0; p < k; ++p)
{
// 1st row of C
C(0, 0) += A(0, p) * B(p, 0);
C(0, 1) += A(0, p) * B(p, 1);
C(0, 2) += A(0, p) * B(p, 2);
C(0, 3) += A(0, p) * B(p, 3);
// 2rd row of C
C(1, 0) += A(1, p) * B(p, 0);
C(1, 1) += A(1, p) * B(p, 1);
C(1, 2) += A(1, p) * B(p, 2);
C(1, 3) += A(1, p) * B(p, 3);
// 3nd row of C
C(2, 0) += A(2, p) * B(p, 0);
C(2, 1) += A(2, p) * B(p, 1);
C(2, 2) += A(2, p) * B(p, 2);
C(2, 3) += A(2, p) * B(p, 3);
// 4th row of C
C(3, 0) += A(3, p) * B(p, 0);
C(3, 1) += A(3, p) * B(p, 1);
C(3, 2) += A(3, p) * B(p, 2);
C(3, 3) += A(3, p) * B(p, 3);
}
}
2.4 4x4 提升 C和A放到Register中
m=n=k<500,性能有2倍提升;m=n=k>500,性能有1.5倍提升。
得益于将A的4行1列和C的4行4列放到寄存器中。当使用超过寄存器容量的寄存器变量时, 性能提升就固定了(即m=n=k>500,性能有1.5倍提升)。
#define A(i, j) a[k*(i) + (j)]
#define B(i, j) a[n*(i) + (j)]
#define C(i, j) a[n*(i) + (j)]
for(int i = 0; i < m; i+=4)
{
for(int j = 0; j < n; j+=4)
{
AddDot4x4(&A(i, 0), &B(0, j), &C(i, j), n, k);
}
}
void AddDot4x4(float *a, float *b, float *c, const int n, const int k)
{
register float
/* hold contributions to
C( 0, 0 ), C( 0, 1 ), C( 0, 2 ), C( 0, 3 )
C( 1, 0 ), C( 1, 1 ), C( 1, 2 ), C( 1, 3 )
C( 2, 0 ), C( 2, 1 ), C( 2, 2 ), C( 2, 3 )
C( 3, 0 ), C( 3, 1 ), C( 3, 2 ), C( 3, 3 ) */
c_00_reg, c_01_reg, c_02_reg, c_03_reg,
c_10_reg, c_11_reg, c_12_reg, c_13_reg,
c_20_reg, c_21_reg, c_22_reg, c_23_reg,
c_30_reg, c_31_reg, c_32_reg, c_33_reg,
/* hold
A( 0, p )
A( 1, p )
A( 2, p )
A( 3, p ) */
a_0p_reg,
a_1p_reg,
a_2p_reg,
a_3p_reg;
c_00_reg = 0.0; c_01_reg = 0.0; c_02_reg = 0.0; c_03_reg = 0.0;
c_10_reg = 0.0; c_11_reg = 0.0; c_12_reg = 0.0; c_13_reg = 0.0;
c_20_reg = 0.0; c_21_reg = 0.0; c_22_reg = 0.0; c_23_reg = 0.0;
c_30_reg = 0.0; c_31_reg = 0.0; c_32_reg = 0.0; c_33_reg = 0.0;
for(int p = 0; p < k; ++p)
{
a_0p_reg = A(0, p);
a_1p_reg = A(1, p);
a_2p_reg = A(2, p);
a_3p_reg = A(3, p);
// 1st row of C
c_00_reg += a_0p_reg * B( p, 0 );
c_01_reg += a_0p_reg * B( p, 1 );
c_02_reg += a_0p_reg * B( p, 2 );
c_03_reg += a_0p_reg * B( p, 3 );
// 2rd row of C
c_10_reg += a_1p_reg * B( p, 0 );
c_11_reg += a_1p_reg * B( p, 1 );
c_12_reg += a_1p_reg * B( p, 2 );
c_13_reg += a_1p_reg * B( p, 3 );
// 3nd row of C
c_20_reg += a_2p_reg * B( p, 0 );
c_21_reg += a_2p_reg * B( p, 1 );
c_22_reg += a_2p_reg * B( p, 2 );
c_23_reg += a_2p_reg * B( p, 3 );
// 4th row of C
c_30_reg += a_3p_reg * B( p, 0 );
c_31_reg += a_3p_reg * B( p, 1 );
c_32_reg += a_3p_reg * B( p, 2 );
c_33_reg += a_3p_reg * B( p, 3 );
}
C( 0, 0 ) += c_00_reg; C( 0, 1 ) += c_01_reg; C( 0, 2 ) += c_02_reg; C( 0, 3 ) += c_03_reg;
C( 1, 0 ) += c_10_reg; C( 1, 1 ) += c_11_reg; C( 1, 2 ) += c_12_reg; C( 1, 3 ) += c_13_reg;
C( 2, 0 ) += c_20_reg; C( 2, 1 ) += c_21_reg; C( 2, 2 ) += c_22_reg; C( 2, 3 ) += c_23_reg;
C( 3, 0 ) += c_30_reg; C( 3, 1 ) += c_31_reg; C( 3, 2 ) += c_32_reg; C( 3, 3 ) += c_33_reg;
}
2.5 4x4 提升 用指针代替循环中的B
轻微性能提升,用指针代替访问B,减少索引开销。
#define A(i, j) a[k*(i) + (j)]
#define B(i, j) a[n*(i) + (j)]
#define C(i, j) a[n*(i) + (j)]
for(int i = 0; i < m; i+=4)
{
for(int j = 0; j < n; j+=4)
{
AddDot4x4(&A(i, 0), &B(0, j), &C(i, j), n, k);
}
}
void AddDot4x4(float *a, float *b, float *c, const int n, const int k)
{
register float
c_00_reg, c_01_reg, c_02_reg, c_03_reg,
c_10_reg, c_11_reg, c_12_reg, c_13_reg,
c_20_reg, c_21_reg, c_22_reg, c_23_reg,
c_30_reg, c_31_reg, c_32_reg, c_33_reg,
a_0p_reg,
a_1p_reg,
a_2p_reg,
a_3p_reg;
float
*b_p0_pntr, *b_p1_pntr, *b_p2_pntr, *b_p3_pntr;
c_00_reg = 0.0; c_01_reg = 0.0; c_02_reg = 0.0; c_03_reg = 0.0;
c_10_reg = 0.0; c_11_reg = 0.0; c_12_reg = 0.0; c_13_reg = 0.0;
c_20_reg = 0.0; c_21_reg = 0.0; c_22_reg = 0.0; c_23_reg = 0.0;
c_30_reg = 0.0; c_31_reg = 0.0; c_32_reg = 0.0; c_33_reg = 0.0;
for(int p = 0; p < k; ++p)
{
a_0p_reg = A(0, p);
a_1p_reg = A(1, p);
a_2p_reg = A(2, p);
a_3p_reg = A(3, p);
b_p0_pntr = &B( p, 0 );
b_p1_pntr = &B( p, 1 );
b_p2_pntr = &B( p, 2 );
b_p3_pntr = &B( p, 3 );
// 1st row of C
c_00_reg += a_0p_reg * *b_p0_pntr;
c_01_reg += a_0p_reg * *b_p1_pntr;
c_02_reg += a_0p_reg * *b_p2_pntr;
c_03_reg += a_0p_reg * *b_p3_pntr;
// 2rd row of C
c_10_reg += a_1p_reg * *b_p0_pntr;
c_11_reg += a_1p_reg * *b_p1_pntr;
c_12_reg += a_1p_reg * *b_p2_pntr;
c_13_reg += a_1p_reg * *b_p3_pntr;
// 3nd row of C
c_20_reg += a_2p_reg * *b_p0_pntr;
c_21_reg += a_2p_reg * *b_p1_pntr;
c_22_reg += a_2p_reg * *b_p2_pntr;
c_23_reg += a_2p_reg * *b_p3_pntr;
// 4th row of C
c_30_reg += a_3p_reg * *b_p0_pntr++;
c_31_reg += a_3p_reg * *b_p1_pntr++;
c_32_reg += a_3p_reg * *b_p2_pntr++;
c_33_reg += a_3p_reg * *b_p3_pntr++;
}
C( 0, 0 ) += c_00_reg; C( 0, 1 ) += c_01_reg; C( 0, 2 ) += c_02_reg; C( 0, 3 ) += c_03_reg;
C( 1, 0 ) += c_10_reg; C( 1, 1 ) += c_11_reg; C( 1, 2 ) += c_12_reg; C( 1, 3 ) += c_13_reg;
C( 2, 0 ) += c_20_reg; C( 2, 1 ) += c_21_reg; C( 2, 2 ) += c_22_reg; C( 2, 3 ) += c_23_reg;
C( 3, 0 ) += c_30_reg; C( 3, 1 ) += c_31_reg; C( 3, 2 ) += c_32_reg; C( 3, 3 ) += c_33_reg;
}
3. 进一步优化4x4(Further optimizing)
3.1 4x4 下降 将循环中的B用指针索引后,放到寄存器
将从B的第j行的指针中,取出的变量放到寄存器中。这样做性能些许下降,但是为了后面能作进一步的优化。
#define A(i, j) a[k*(i) + (j)]
#define B(i, j) a[n*(i) + (j)]
#define C(i, j) a[n*(i) + (j)]
for(int i = 0; i < m; i+=4)
{
for(int j = 0; j < n; j+=4)
{
AddDot4x4(&A(i, 0), &B(0, j), &C(i, j), n, k);
}
}
void AddDot4x4(float *a, float *b, float *c, const int n, const int k)
{
register float
c_00_reg, c_01_reg, c_02_reg, c_03_reg,
c_10_reg, c_11_reg, c_12_reg, c_13_reg,
c_20_reg, c_21_reg, c_22_reg, c_23_reg,
c_30_reg, c_31_reg, c_32_reg, c_33_reg,
a_0p_reg,
a_1p_reg,
a_2p_reg,
a_3p_reg,
b_p0_reg,
b_p1_reg,
b_p2_reg,
b_p3_reg;
float
*b_p0_pntr, *b_p1_pntr, *b_p2_pntr, *b_p3_pntr;
b_p0_pntr = &B( 0, 0 );
b_p1_pntr = &B( 0, 1 );
b_p2_pntr = &B( 0, 2 );
b_p3_pntr = &B( 0, 3 );
c_00_reg = 0.0; c_01_reg = 0.0; c_02_reg = 0.0; c_03_reg = 0.0;
c_10_reg = 0.0; c_11_reg = 0.0; c_12_reg = 0.0; c_13_reg = 0.0;
c_20_reg = 0.0; c_21_reg = 0.0; c_22_reg = 0.0; c_23_reg = 0.0;
c_30_reg = 0.0; c_31_reg = 0.0; c_32_reg = 0.0; c_33_reg = 0.0;
for(int p = 0; p < k; ++p)
{
a_0p_reg = A(0, p);
a_1p_reg = A(1, p);
a_2p_reg = A(2, p);
a_3p_reg = A(3, p);
b_p0_reg = *b_p0_pntr++;
b_p1_reg = *b_p1_pntr++;
b_p2_reg = *b_p2_pntr++;
b_p3_reg = *b_p3_pntr++;
// 1st row of C
c_00_reg += a_0p_reg * b_p0_reg;
c_01_reg += a_0p_reg * b_p1_reg;
c_02_reg += a_0p_reg * b_p2_reg;
c_03_reg += a_0p_reg * b_p3_reg;
// 2nd row of C
c_10_reg += a_1p_reg * b_p0_reg;
c_11_reg += a_1p_reg * b_p1_reg;
c_12_reg += a_1p_reg * b_p2_reg;
c_13_reg += a_1p_reg * b_p3_reg;
// 3rd row of C
c_20_reg += a_2p_reg * b_p0_reg;
c_21_reg += a_2p_reg * b_p1_reg;
c_22_reg += a_2p_reg * b_p2_reg;
c_23_reg += a_2p_reg * b_p3_reg;
// 4th row of C
c_30_reg += a_3p_reg * b_p0_reg;
c_31_reg += a_3p_reg * b_p1_reg;
c_32_reg += a_3p_reg * b_p2_reg;
c_33_reg += a_3p_reg * b_p3_reg;
}
C( 0, 0 ) += c_00_reg; C( 0, 1 ) += c_01_reg; C( 0, 2 ) += c_02_reg; C( 0, 3 ) += c_03_reg;
C( 1, 0 ) += c_10_reg; C( 1, 1 ) += c_11_reg; C( 1, 2 ) += c_12_reg; C( 1, 3 ) += c_13_reg;
C( 2, 0 ) += c_20_reg; C( 2, 1 ) += c_21_reg; C( 2, 2 ) += c_22_reg; C( 2, 3 ) += c_23_reg;
C( 3, 0 ) += c_30_reg; C( 3, 1 ) += c_31_reg; C( 3, 2 ) += c_32_reg; C( 3, 3 ) += c_33_reg;
}
3.2 4x4 提升 变为vector operation进一步转为intrinsic
规模m=n=k<500下,基本都有2~3倍的性能提升(但规模在m=n=k>500下,则几乎没有提升,后面将讲到如何优化使用L2 Cache来做更大规模的提升),提升的原因是用上了向量寄存器和向量操作(或者说是SIMD)。这个实现过程,先考虑后续intrinsic的写法,即先写成对应的不用intrinsic的代码,然后再转成intrinsic函数。
实现过程中参考这个double的4x4的做法:Optimization_4x4_9 · flame/how-to-optimize-gemm Wiki,但是这种情况与我们的不同:1. 咱们是float;2. 咱们是行优先。
因此,对B按行取4个的前提下,对于矩阵A在取数时有如下三个思路:

对B按行取4个的前提下,有三个对A处理的思路:
- 每次取A的第1列的4个,与B的第1行的4个,即两个float4。因行优先,对B来说是连续的,对A则需要逐个元素竖着排布拼成float4;
- 取A行的第1个元素,重复4次,即float4,这样取A的四行,得到4个float4;
- 对B转置为B_trans,与A操作一样,按照行取4行(实际为B的4列);或相反,对A转置为A_trans,则与B操作一样。
我实现的是第二种,即对A中的元素进行重复,如下是实现代码:
#define A(i, j) a[k*(i) + (j)]
#define B(i, j) a[n*(i) + (j)]
#define C(i, j) a[n*(i) + (j)]
for(int i = 0; i < m; i+=4)
{
for(int j = 0; j < n; j+=4)
{
AddDot4x4(&A(i, 0), &B(0, j), &C(i, j), n, k);
}
}
#include <mmintrin.h>
#include <xmmintrin.h> // SSE
#include <pmmintrin.h> // SSE2
#include <emmintrin.h> // SSE3
typedef union v4f
{
__m128 v;
float s[4];
} v4f_t;
void AddDot4x4(float *a, float *b, float *c, const int n, const int k)
{
v4f_t
c_00_01_02_03_vreg,
c_10_11_12_13_vreg,
c_20_21_22_23_vreg,
c_30_31_32_33_vreg,
b_p0_p1_p2_p3_vreg,
a_0p_x4_vreg,
a_1p_x4_vreg,
a_2p_x4_vreg,
a_3p_x4_vreg;
float
*b_p0_pntr = &B( 0, 0 );
c_00_01_02_03_vreg.v = _mm_setzero_ps();
c_10_11_12_13_vreg.v = _mm_setzero_ps();
c_20_21_22_23_vreg.v = _mm_setzero_ps();
c_30_31_32_33_vreg.v = _mm_setzero_ps();
for(int p = 0; p < k; ++p)
{
// duplicate each element in A as float4
a_0p_x4_vreg.v = __mm_loaddup_ps( (float *) &A( 0, p ) );
a_1p_x4_vreg.v = __mm_loaddup_ps( (float *) &A( 1, p ) );
a_2p_x4_vreg.v = __mm_loaddup_ps( (float *) &A( 2, p ) );
a_3p_x4_vreg.v = __mm_loaddup_ps( (float *) &A( 3, p ) );
b_p0_pntr += p * n;
b_p0_p1_p2_p3_vreg.v = __mm_load_ps( (float *) b_p0_pntr );
c_00_01_02_03_vreg.v += a_0p_x4_vreg.v * b_p0_p1_p2_p3_vreg.v;
c_10_11_12_13_vreg.v += a_1p_x4_vreg.v * b_p0_p1_p2_p3_vreg.v;
c_20_21_22_23_vreg.v += a_2p_x4_vreg.v * b_p0_p1_p2_p3_vreg.v;
c_30_31_32_33_vreg.v += a_3p_x4_vreg.v * b_p0_p1_p2_p3_vreg.v;
}
// 1st row of C
C( 0, 0 ) += c_00_01_02_03_vreg.s[0];
C( 0, 1 ) += c_00_01_02_03_vreg.s[1];
C( 0, 2 ) += c_00_01_02_03_vreg.s[2];
C( 0, 3 ) += c_00_01_02_03_vreg.s[3];
// 2nd row of C
C( 1, 0 ) += c_10_11_12_13_vreg.s[0];
C( 1, 1 ) += c_10_11_12_13_vreg.s[1];
C( 1, 2 ) += c_10_11_12_13_vreg.s[2];
C( 1, 3 ) += c_10_11_12_13_vreg.s[3];
// 3rd row of C
C( 2, 0 ) += c_20_11_12_13_vreg.s[0];
C( 2, 1 ) += c_20_11_12_13_vreg.s[1];
C( 2, 2 ) += c_20_11_12_13_vreg.s[2];
C( 2, 3 ) += c_20_11_12_13_vreg.s[3];
// 4th row of C
C( 3, 0 ) += c_30_31_32_33_vreg.s[0];
C( 3, 1 ) += c_30_31_32_33_vreg.s[1];
C( 3, 2 ) += c_30_31_32_33_vreg.s[2];
C( 3, 3 ) += c_30_31_32_33_vreg.s[3];
}
英特尔® 高级矢量扩展指令集简介
-
[英特尔® 高级矢量扩展指令集简介 英特尔® 软件](https://software.intel.com/zh-cn/articles/introduction-to-intel-advanced-vector-extensions) - Intel Intrinsics Guide
-
[Technologies NEON Intrinsics Reference – Arm Developer](https://developer.arm.com/technologies/neon/intrinsics)
Optimization Notice
虽然针对非英特尔处理器也有优化,但不保证有效,具体参考_用户和参考指南_,其中包括了本注意事项涵盖的特定指令集的更多相关信息。
英特尔® 高级矢量扩展指令集(英特尔® AVX)是在英特尔® 架构 CPU 上执行单指令多数据 (SIMD) 运算的指令集。这些指令添加了以下特性,对之前的 SIMD 产品——MMX™ 指令和英特尔® 数据流单指令多数据扩展指令集(英特尔® SSE)进行了扩展:
- 将 128 位 SIMD 寄存器扩展至 256 位。英特尔® AVX 的目标是在未来可以支持 512 或 1024 位。
- 添加了 3 操作数非破坏性运算。之前在 A = A + B 类运算中执行的是 2 操作数指令,它将覆盖源操作数,而新的操作数可以执行 A = B + C 类运算,且保持原始源操作数不变。.
- 少数几个指令采用 4 寄存器操作数,通过移除不必要的指令,支持更小、更快的代码。
- 对于操作数的内存对齐要求有所放宽。
- 新的扩展编码方案 (VEX) 旨在使得以后添加更加容易以及所执行的指令编码更小、速度更快。
与这些改进密切相关的是新的融合乘加 (FMA) 指令,它可以更快、更精确地执行专门运算,例如单指令 A = A * B + C。第二代英特尔® 酷睿™ CPU 中将可提供 FMA 指令。其他特性还包括处理高级加密标准 (AES) 加密和解密的指令、用于某些加密基元的紧缩 carry-less 乘法运算 (PCLMULQDQ) 以及某些用于未来指令的预留槽,如硬件随机数生成器。
指令集概述
新指令使用英特尔的 VEX prefix 进行编码,VEX prefix 是一个 2个或 3 个字节的前缀,旨在降低当前和未来 x86/x64 指令编码的复杂性。两个新的 VEX prefix 形成于两个过时的 32 位指令——使用 DS 的 Load Pointer(LDS-0xC4,3 字节形式)和使用 ES 的 Load Pointer(LES-0xC5, 2 字节形式),它们以 32 位模式加载 DS 和 ES 段寄存器。在 64 位模式中,操作码 LDS 和 LES 生成一个无效操作码异常,但是在英特尔® AVX 下,这些操作码可另外用作编码新指令前缀。最终,VEX 指令只能在 64 位模式中运行时使用。前缀可比之前的 x86 指令编码更多的寄存器,可用于访问新的 256 位 SIMD 寄存器或者使用 3 和 4 操作数语法。作为用户,您无需担心这个问题(除非您正在编写汇编器或反汇编器)。
注:下文假定运算都是在 64 位模式中进行。
SIMD 指令可以在一个单一步骤中处理多个片段的数据,加速许多任务的吞吐量,包括视频编解码、图像处理、数据分析和物理模拟。在 32 位长度(称之为单精度)和64 位长度(称之为双精度)中,英特尔® AVX 指令在IEEE-754浮点值上运行。IEEE-754 是一个标准定义的、可复制的强大浮点运算,是大多数主流数字计算的标准。
较早的相关英特尔® SSE 指令还支持各种带符号和无符号整数大小,包括带符号和无符号字节(B,8 位)、字(W,16 位)、双字(DW,32 位)、四字(QW,64 位)和双四字(DQ,128 位)长度。并非所有指令都适用于所有大小组合,更多详细信息,敬请参阅“更多信息”中提供的链接。请参阅本文后文中的图 2,了解数据类型的图形表示法。
支持英特尔® AVX(和 FMA)的硬件包括 16 个 256 位 YMM 寄存器 YMM0-YMM15 和一个名为 MXCSR的 32 位控制/状态寄存器。YMM 寄存器替代了英特尔® SSE 使用的较早的 128 位 XMM 寄存器,它将 XMM 寄存器视作相应 YMM 寄存器的下层部分,如图 1 所示。

图 1. XMM 寄存器覆盖 YMM 寄存器。
MXCSR 的 0-5 位显示设置“粘滞”位后 SIMD 浮点异常,除非使用位LDMXCSR 或 FXRSTOR清除,否则它们将一直保持设置。设置时 7-12 位屏蔽个体异常,可通过启动进行初始设置或重置。0-5 位分别显示为无效运算、非法、被零除、溢出和精度。如欲获取详细信息,请参阅“更多信息”部分提供的链接。
图 2 显示了英特尔® SSE 和英特尔® AVX 指令中使用的数据类型。对于英特尔® AVX,允许使用增加至 128 或 256 位的 32 位或 64 位浮点类型的倍数以及增加至 128 位的任意整数类型的倍数。

图 2.英特尔® AVX 和英特尔® SSE 数据类型
指令通常分为标量版本和矢量版本,如图 3 所示。矢量版本通过将数据以并行“SIMD”模式在寄存器中处理进行运算;而标量版本则只在每个寄存器的一个条目中进行运算。这一区别减少了某些算法中的数据移动,提供了更加出色的整体吞吐量。

图 3. SIMD 与标量运算
内存对齐
当数据以 n 字节内存界限上存储的 n 字节块进行运算时,数据为内存对齐数据。例如,将 256 位数据加载至 YMM 寄存器中时,如果数据源为 256 位对齐,则数据被称为“对齐”.
对于英特尔® SSE 运算,除非明确规定,否则都需要内存对齐。例如,在英特尔® SSE 下,有针对内存对齐和内存未对齐运算的特定指令,如MOVAPD(移动对齐的紧缩双精度值)和 MOVUPD(移动非对齐的紧缩双精度值)指令。没有像这样分为两个的指令需要执行对齐访问。
英特尔® AVX 已经放宽了某些内存对齐要求,因此默认情况下,英特尔® AVX 允许未对齐的访问;但是,这样的访问将导致性能下降,因此旨在要求数据保持内存对齐的原规则仍然是不错的选择(面向 128 位访问的 16 位对齐和面向 256 位访问的 32 位对齐)。主要例外是明确指出需要内存对齐数据的 SSE 指令的VEX 扩展版本:这些指令仍然要求使用对齐的数据。其他要求对齐访问的特定指令请参阅英特尔® 高级矢量扩展指令集编程指南中的表2.4(请参阅“更多信息”中提供的链接)。
除了未对齐数据问题外,另外一个性能问题是混合使用旧的仅 XMM 的指令和较新的英特尔® AVX 指令会导致延迟,因此需要最大限度地控制 VEX 编码指令和旧的英特尔® SSE 代码之间的转换。也就是说,不要将 VEX 前缀的指令和非 VEX 前缀的指令混合使用,以实现最佳吞吐量。如果您非要这么做,请对同一 VEX/非 VEX 级别的指令进行分组,最大限度地控制二者之间的转换。此外,如果上层 YMM 位通过 VZEROUPPER 或 VZEROALL 设置为零(编译器应自动插入),则无转换损失。该插入要求另外一个指令,因此推荐使用分析 (profiling)。
4. 4x4 提升 利用L2 Cache对矩阵blocking
4.1 参考代码分析
参考:Optimization_4x4_11 · flame/how-to-optimize-gemm Wiki
对于参考代码的分析,参考代码更新后,规模在m=n=k>500有2倍率性能提升,对矩阵C做blocking(每次内层循环InnerKernel计算一块规模为mc x n大小的矩阵C,但并没有完全算完,只算了pb/k * ib/m,其中pb = min( k-p, kc ), ib = min( m-i, mc ))。对矩阵的分块充分利用L2 Cache。
/* Block sizes */
#define mc 256
#define kc 128
/* This time, we compute a mc x n block of C by a call to the InnerKernel */
for ( p=0; p<k; p+=kc ){
pb = min( k-p, kc );
for ( i=0; i<m; i+=mc ){
ib = min( m-i, mc );
InnerKernel( ib, n, pb, &A( i,p ), lda, &B(p, 0 ), ldb, &C( i,0 ), ldc );
}
}
外层的两个循环改为对k(矩阵A的列、B的行)和m(矩阵A的行)的遍历,同时分别设定这两个遍历的自增值kc、mc,每次调用完一个InnerKernel,即得到一块大小为mc x n的C矩阵元素。但该过程并没有将这一块大小为mc x n的C矩阵元素的结果算完(因为对k遍历的for循环在最外层)。
对由于分块带来的变化的分析(kc和mc):
- 把原本的
AddDot4x4作为micro kernel放到InnerKernel中,InnerKernel作为kernel; - 每次内层循环
InnerKernel计算一块规模为mc x n大小的矩阵C,但并没有完全算完,只算了pb/k,其中pb = min( k-p, kc )。pb作为最内层新的k; pb = min( k-p, kc )和ib = min( m-i, mc )是用来处理最后剩下的边界问题;- 外层两个
for循环遍历的是k和m,每次自增大小分别为kc和mc(这也是矩阵分块blocking的大小),进一步有pb = min( k-p, kc )和ib = min( m-i, mc ); InnerKernel中两个for循环遍历的是m和n,每次自增均为4(前文中提到,这个值自己可以调);AddDot4x4中的循环,每次自增1,和上一次的代码没有变化,但需要注意传进来的k值不是矩阵A的列数(B的行数),而是pb,即一个AddDot4x4,对矩阵C中的元素只算了pb/k,其中pb = min( k-p, kc ),此外AddDot4x4本身被InnerKernel(行列自增值都为4)调用,每次算C矩阵具体到每个元素的完成度只有:4x4xpb,即A的4行的前pb列,B的4列的前pb行,其中pb = min( k-p, kc )。
4.2 对现有代码加入blocking
考虑到参考代码是列优先,我们是行优先,那么需要对矩阵C做blocking时,做以下变化,同时修改变量名,如inc_p,inc_j,更清晰:
/* Block sizes */
#define inc_j 256 // inc_j along n
#define inc_p 128 // inc_p along k
#define min( i, j ) ( (i)<(j) ? (i): (j) )
/* This time, we compute a m x block_n block of C by a call to the InnerKernel */
for ( p=0; p<k; p+=inc_p )
{
block_k = min( k-p, inc_p );
for ( j=0; j<n; j+=inc_j )
{
block_n = min( n-j, inc_j );
InnerKernel( m, block_n, block_k, &A( i,p ), lda, &B(p, 0 ), ldb, &C( i,0 ), ldc );
}
}
#define A(i, j) a[lda*(i) + (j)]
#define B(i, j) b[ldb*(i) + (j)]
#define C(i, j) c[ldc*(i) + (j)]
/* Block sizes */
#define inc_j 256 // inc_j along n
#define inc_p 128 // inc_p along k
#define min( i, j ) ( (i)<(j) ? (i): (j) )
/* This time, we compute a m x block_n block of C by a call to the InnerKernel */
for ( p=0; p<k; p+=inc_p )
{
block_k = min( k-p, inc_p );
for ( j=0; j<n; j+=inc_j )
{
block_n = min( n-j, inc_j );
InnerKernel( m, block_n, block_k, &A( i,p ), lda, &B(p, 0 ), ldb, &C( i,0 ), ldc );
}
}
void InnerKernel( const int m, const int n, const int k,
float *a, const int lda,
float *b, const int ldb,
float *c, const int ldc )
{
for( int i=0; i<m; i+=4 )
{
for( int j=0; j<n; j+=4 )
{
AddDot4x4( k, &A( i,0 ), lda, &B( 0,j ), ldb, &C( i,j ), ldc );
}
}
}
#include <mmintrin.h>
#include <xmmintrin.h> // SSE
#include <pmmintrin.h> // SSE2
#include <emmintrin.h> // SSE3
typedef union v4f
{
__m128 v;
float s[4];
} v4f_t;
void AddDot4x4( const int k,
float *a, const int lda,
float *b, const int ldb,
float *c, const int ldc)
{
v4f_t
c_00_01_02_03_vreg,
c_10_11_12_13_vreg,
c_20_21_22_23_vreg,
c_30_31_32_33_vreg,
b_p0_p1_p2_p3_vreg,
a_0p_x4_vreg,
a_1p_x4_vreg,
a_2p_x4_vreg,
a_3p_x4_vreg;
float
*b_p0_pntr = &B( 0, 0 );
c_00_01_02_03_vreg.v = _mm_setzero_ps();
c_10_11_12_13_vreg.v = _mm_setzero_ps();
c_20_21_22_23_vreg.v = _mm_setzero_ps();
c_30_31_32_33_vreg.v = _mm_setzero_ps();
for(int p = 0; p < k; ++p)
{
// duplicate each element in A as float4
a_0p_x4_vreg.v = __mm_loaddup_ps( (float *) &A( 0, p ) );
a_1p_x4_vreg.v = __mm_loaddup_ps( (float *) &A( 1, p ) );
a_2p_x4_vreg.v = __mm_loaddup_ps( (float *) &A( 2, p ) );
a_3p_x4_vreg.v = __mm_loaddup_ps( (float *) &A( 3, p ) );
b_p0_pntr += p * n;
b_p0_p1_p2_p3_vreg.v = __mm_load_ps( (float *) b_p0_pntr );
c_00_01_02_03_vreg.v += a_0p_x4_vreg.v * b_p0_p1_p2_p3_vreg.v;
c_10_11_12_13_vreg.v += a_1p_x4_vreg.v * b_p0_p1_p2_p3_vreg.v;
c_20_21_22_23_vreg.v += a_2p_x4_vreg.v * b_p0_p1_p2_p3_vreg.v;
c_30_31_32_33_vreg.v += a_3p_x4_vreg.v * b_p0_p1_p2_p3_vreg.v;
}
// 1st row of C
C( 0, 0 ) += c_00_01_02_03_vreg.s[0];
C( 0, 1 ) += c_00_01_02_03_vreg.s[1];
C( 0, 2 ) += c_00_01_02_03_vreg.s[2];
C( 0, 3 ) += c_00_01_02_03_vreg.s[3];
// 2nd row of C
C( 1, 0 ) += c_10_11_12_13_vreg.s[0];
C( 1, 1 ) += c_10_11_12_13_vreg.s[1];
C( 1, 2 ) += c_10_11_12_13_vreg.s[2];
C( 1, 3 ) += c_10_11_12_13_vreg.s[3];
// 3rd row of C
C( 2, 0 ) += c_20_11_12_13_vreg.s[0];
C( 2, 1 ) += c_20_11_12_13_vreg.s[1];
C( 2, 2 ) += c_20_11_12_13_vreg.s[2];
C( 2, 3 ) += c_20_11_12_13_vreg.s[3];
// 4th row of C
C( 3, 0 ) += c_30_31_32_33_vreg.s[0];
C( 3, 1 ) += c_30_31_32_33_vreg.s[1];
C( 3, 2 ) += c_30_31_32_33_vreg.s[2];
C( 3, 3 ) += c_30_31_32_33_vreg.s[3];
}
